Bellman-Ford Algorithm – Enhanced Explanation with Proofs
What is the Bellman-Ford Algorithm?
The Bellman-Ford algorithm is a method to find the shortest paths from a single source vertex to all other vertices in a weighted directed graph.
It works even when some edges have negative weights. This makes it more powerful than Dijkstra’s algorithm, which does not work with negative edge weights.
Bellman-Ford can also detect negative weight cycles (cycles where the total weight is negative), which means that the shortest path does not exist because it can keep decreasing forever.
When to Use It
- You want to find shortest paths from one starting point.
- Some edges have negative weights.
- You need to check if the graph has a negative weight cycle.
Basic Idea
The algorithm works by relaxing the edges multiple times.
What is "Relaxing" an Edge?
Suppose there is an edge from node u to node v with weight w.
If the shortest known distance to u is d[u], and going from u to v is shorter than the current known distance to v, we update it:
if d[u] + w < d[v] then
d[v] = d[u] + w
Edge Relaxation Illustration:
We do this again and again until no more updates are needed.
Step-by-Step Algorithm
Let the number of vertices be n and the number of edges be m.
- Set the distance to the source node to 0, and all others to infinity.
- Repeat the following step n - 1 times:
- For every edge (u, v) with weight w:
- If d[u] + w < d[v], update d[v] = d[u] + w.
- For every edge (u, v) with weight w:
- To check for negative cycles:
- Repeat the edge loop one more time.
- If any d[v] gets updated, then there is a negative weight cycle.
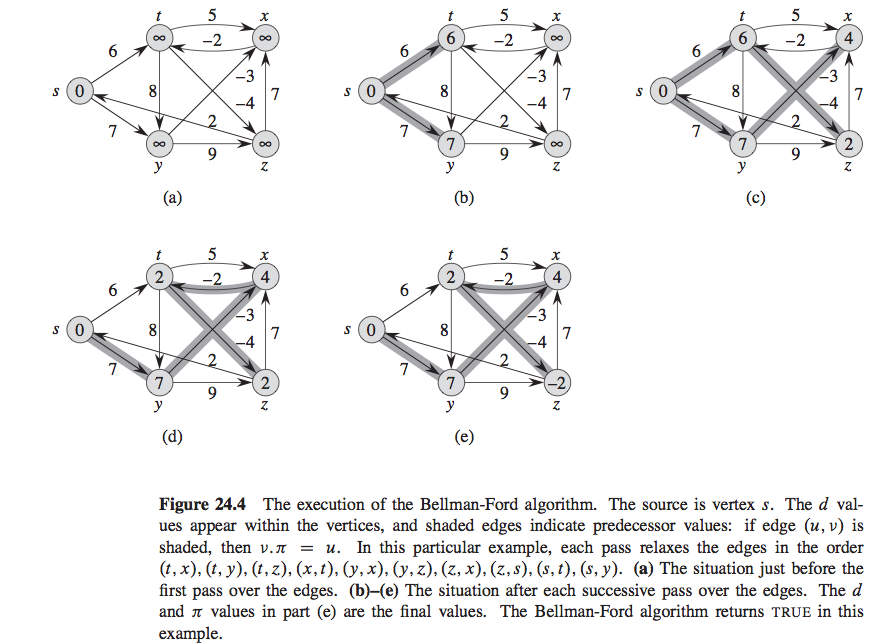
Bellman-Ford Algorithm Visualization:

Implementation in Pseudocode
const int INF = 1e9;
struct edge {
int u, v, cost;
};
vector<edge> edges;
vector<int> dist(n, INF);
dist[source] = 0;
// Step 2: Relax all edges n - 1 times
for (int i = 0; i < n - 1; ++i) {
for (edge e : edges) {
if (dist[e.u] < INF && dist[e.v] > dist[e.u] + e.cost) {
dist[e.v] = dist[e.u] + e.cost;
}
}
}
// Step 3: Check for negative weight cycles
bool hasNegativeCycle = false;
for (edge e : edges) {
if (dist[e.u] < INF && dist[e.v] > dist[e.u] + e.cost) {
hasNegativeCycle = true;
break;
}
}
Why It Works – Proof
Goal: After running the algorithm, dist[v] should hold the shortest distance from the source to vertex v.
Assumptions: The graph does not contain negative weight cycles.
Proof: Any shortest path from the source to a node contains at most n - 1 edges, because a simple path can’t repeat a node and the graph has n nodes. Each time we relax all edges, we allow paths of one more edge than before.
- After the 1st pass: shortest paths with 1 edge are correct.
- After the 2nd pass: shortest paths with 2 edges are correct.
- ...
- After n - 1 passes: all shortest paths (with at most n - 1 edges) are correct.
Thus, by doing n - 1 passes, we are guaranteed to have found all shortest paths, as long as there are no negative cycles.
Negative Cycle Detection:
If we run the algorithm one more time (the nth time) and any distance still changes, this means there is a cycle that keeps reducing the distance. That is, there is a negative weight cycle.
Negative Cycle Example:
Consider a graph with vertices A, B, and C, with edges A->B (-2), B->C (-3), and C->A (-2). The sum of the weights is -7, indicating a negative cycle. The Bellman-Ford algorithm will detect this because the distances will continue to decrease after the (n-1)th iteration.
How to Find the Shortest Path Itself
We can keep track of the parent (or predecessor) of each node. Whenever we update dist[v], we also update parent[v] = u. To get the path from source to v:
- Start at v, go to parent[v], then to parent[parent[v]], and so on.
- Stop when you reach the source (or -1 if unreachable).
- Reverse the path to get the correct order.
Time and Space Complexity
- Time: O(n * m), where n is the number of vertices, and m is the number of edges.
- Space: O(n), for storing distances and parents.
Comparison with Dijkstra's Algorithm
| Feature | Bellman-Ford | Dijkstra's Algorithm |
|---|---|---|
| Negative Weights | Yes | No |
| Negative Cycles | Detects | No |
| Time Complexity | O(n * m) | O((V + E) log V) using a priority queue |
| Use Cases | Graphs with negative weights, cycle detection | Graphs with non-negative weights, shortest paths |
| Implementation | Simpler | More complex |
Example
Graph:
Vertices: 0, 1, 2
Edges:
0 → 1 (weight 4)
0 → 2 (weight 5)
1 → 2 (weight -2)
Run Bellman-Ford from source 0.
Start:
dist = 0
dist = INF
dist = INF
First pass:
0→1: 0 + 4 = 4 → dist = 4
0→2: 0 + 5 = 5 → dist = 5
1→2: 4 + (-2) = 2 → dist = 2
Second pass:
No further updates → done.
Final distances:
dist = 0
dist = 4
dist = 2
Problem and Solution Explanation: Problem 423 - MPI Maelstrom
Problem Description:
The problem "MPI Maelstrom" (Problem 423) on Online Judge involves finding the shortest paths in a network represented as an adjacency matrix. The network describes connections between nodes, with edge weights representing communication costs. The goal is to determine the minimum cost for a message to be broadcast from a source node (node 1) to all other nodes in the network. Note that the input graph will not have negative weight cycles.
Solution Explanation:
This problem is a classic application of the single-source shortest path problem. Since the problem guarantees no negative weight cycles, Dijkstra's algorithm would typically be the go-to solution. However, since the document is about the Bellman-Ford algorithm, we can use it here.
Here's how Bellman-Ford can be applied to solve this problem:
Input Processing:
- Read the number of nodes, n, from the input.
- Create an adjacency matrix to represent the network. Initialize the matrix. The diagonal elements (cost from a node to itself) are 0. The input provides the upper triangle of the matrix. For entries where no direct connection is given, we can assume a large value (representing infinity) to indicate no direct path. We need to populate the lower triangle of the matrix by reflecting the values from the upper triangle since the graph is undirected.
Initialization:
- Create a distance array, dist, of size n. Initialize all elements to infinity (a large value) except dist[0] (distance from node 1 to itself), which is set to 0.
Bellman-Ford Algorithm:
- Iterate n - 1 times. In each iteration, iterate through all possible edges in the graph.
- For each edge (u, v) with weight w (cost from the adjacency matrix), relax the edge: If dist[u] + w < dist[v], update dist[v] to dist[u] + w.
Output:
- After the iterations, the dist array will contain the shortest distances from node 1 to all other nodes. Find the maximum value in the dist array, as the problem asks for the minimum cost to reach all nodes. Print this maximum value.
Why Bellman-Ford Works Here:
- Single Source Shortest Path: We need to find the shortest path from a single source (node 1) to all other nodes.
- No Negative Weight Cycles: The problem statement guarantees no negative weight cycles, which is a requirement for Bellman-Ford to find the correct shortest paths.
- Correctness: After n - 1 iterations, Bellman-Ford guarantees finding the shortest paths in a graph without negative cycles.
Key Points:
- The problem uses 1-based indexing, but the solution and code use 0-based indexing.
- The algorithm efficiently handles the graph represented as an adjacency matrix.
- The final answer is the maximum of all shortest paths from the source to all other nodes.
Code Solution (C++)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int INF = 1e9;
int main() {
int n;
cin >> n;
// Create adjacency matrix
vector<vector<int>> adj_matrix(n, vector<int>(n, INF));
for (int i = 0; i < n; ++i) {
adj_matrix[i][i] = 0; // Distance from node to itself is 0
}
// Read upper triangle of the matrix
for (int i = 1; i < n; ++i) {
for (int j = 0; j < i; ++j) {
string cost_str;
cin >> cost_str;
if (cost_str != "x") {
int cost = stoi(cost_str);
adj_matrix[i][j] = cost;
adj_matrix[j][i] = cost; // Copy to lower triangle
}
}
}
// Initialize distances
vector<int> dist(n, INF);
dist[0] = 0; // Distance from node 1 (0-indexed) to itself is 0
// Bellman-Ford
for (int i = 0; i < n - 1; ++i) {
for (int u = 0; u < n; ++u) {
for (int v = 0; v < n; ++v) {
if (adj_matrix[u][v] != INF && dist[u] != INF && dist[u] + adj_matrix[u][v] < dist[v]) {
dist[v] = dist[u] + adj_matrix[u][v];
}
}
}
}
// Find the maximum distance
int max_dist = 0;
for (int i = 0; i < n; ++i) {
max_dist = max(max_dist, dist[i]);
}
cout << max_dist << endl;
return 0;
}
Explanation of the Code:
- Include Headers: Includes the necessary iostream, vector, and algorithm headers.
- Constants and Namespaces: Defines INF and uses the standard namespace.
-
Main Function:
- Reads the number of nodes, n.
- Creates an adjacency matrix adj_matrix of size n x n and initializes it.
- Reads the input for the upper triangle of the adjacency matrix and populates the lower triangle.
- Initializes the distance vector dist.
- Implements the Bellman-Ford algorithm.
- Finds the maximum distance in the dist vector.
- Prints the maximum distance.
Real-World Applications
- Network Routing: Bellman-Ford is used in distance-vector routing protocols to find the best routes for data packets in a network. Routers use it to determine the shortest path to other networks.
- Currency Exchange: Bellman-Ford can be used to detect arbitrage opportunities in currency exchange markets. If a sequence of exchanges results in a profit, it indicates a negative weight cycle.
Summary
- Bellman-Ford is used to find shortest paths from a source.
- It works with negative weights.
- It detects negative weight cycles.
- It runs in O(n * m) time.
- It uses edge relaxation up to n - 1 times.
- It is simpler but slower than Dijkstra's for graphs without negative weights.